Et eksempel
La oss tenke oss at du skal lage terrasse eller hagestue. Hvordan kan du være sikker på at den blir liggende vinkelrett på den eksisterende hytta?
 |
| Det er ikke vanskelig å lage en rett vinkel |
Regnestykket er enkelt
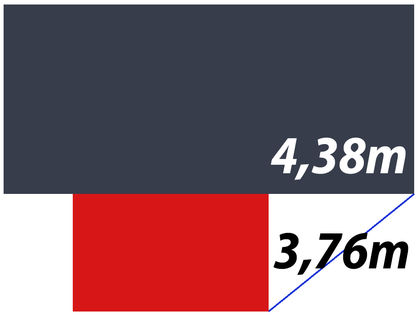
I eksemplet vårt starter nybygget 4,38 meter fra hjørnet på hytta og skal 3,76 meter ut fra denne.
De to nevnte målene er katetene i en rettvinklet trekant, mens linja vi har markert med blått, er hypotenusen.
Da har vi følgende formel:
katet12 + katet22 = hypotenus2
4,38 . 4,38 + 3,76 . 3,76 = 19,1844 + 14,1376 = 33,322
Altså er hypotenusen ganget med seg selv 33,322, og kvadratroten av 33,322 er omtrent 5,77.
Altså, når du har lagt grunnmuren slik at den blå linja på figuren er 5,77 meter, er du sikker på at den rette vinkelen virkelig er rett.
 |
| Når to og to sider er parvis like lange og diagonalene er like, er bygget vinkelrett. |
Tilbygget må jo også være vinkelrett
Det er ikke nok at nybygget står vinkelrett på hytta. Selve nybygget må jo også være vinkelrett.
Da gjelder det å finne diagonalene fra hjørne til hjørne.
katet12 + katet22 = hypotenus2
4,80 . 4,80 + 3,76 . 3,76 = 23,0400 + 14,1376 = 37,1776
Da blir hypotenusen, det vil si diagonalene 6,10, altså 6,10 meter.
Som en ekstra sjekk måler du begge diagonalene og alle de fire sidene. Hvis to og to motstående sider er parvis like lange og diagonalene er helt like, er det riktig.
3 - 4 - 5 -trikset
Hvis de bare skal sjekke en vinkel, er det mange snekkere som bruker forholdet mellom tallene 3, 4 og 5 som hjelp, fordi
32 + 42 = 52
9 + 16 = 25
Altså, hvis de to katetene er 3 og 4 meter, må hypotenusen være 5.
Du oppnår akkurat det samme om du dobler eller halverer, fordi
62 + 82 = 102
1,52 + 2,02 = 2,52
Lykke til.










